You may be wondering if there's an opposite to powers of 10; something like how division is the opposite of multiplication or subtraction is the opposite of addition. Well, it turns out that there is just such a thing: logarithms. It used to be that logs were really important for multiplying and dividing, and were used all the time in doing arithmetic using slide rules. Now that hand calculators are incredibly commonplace, the use of logarithms for basic calculations is fading away, but it can still be worthwhile. And while using logarithms for simple arithmetic is uncommon, there are other uses for logarithms in many areas of science, and we may see some of these uses later in the class.
The logarithm (log) of a number written as a power of 10 is really easy to
calculate. It's just the exponent. So, for example, the log of 
is
3. The log of 
is just -2. And swapping that around is also easy:
if I tell you the log of some number is 6, all you have to do is say the number
is 
, or one million. Some more examples:
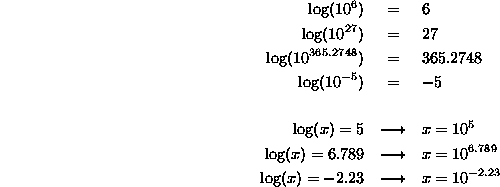
Where logs are really useful is in doing multiplication and division of numbers. You know from the previous section that to multiply numbers which are powers of 10, you add the exponents, and to divide such numbers, you subtract the exponents. Well, since the log of a number which is a power of 10 is just the exponent for that power, to do multiplication, you just add the logs. To do division, just subtract the logs. An example:
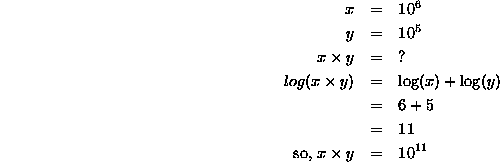
You could have seen the answer from the previous section, but you can see how easy it is to do this using logs. And so you can probably see why, back before powerful computers, logarithms made complicated computations simpler. As I said, few people do multiplication this way anymore, but it can be done.