Numbers written in scientific notation are still just numbers, so of course you can do arithmetic on them. Doing arithmetic using scientific notation seems more complicated than the usual method when you've never done it before, but after a little practice, it's actually easier. That's particularly true for multiplication and division, so we'll skip addition and subtraction and go straight to multiplying and dividing.
Let's look at an example. What is
? To answer this question, first,
let's shuffle the numbers a bit:
Nothing fancy here, but I think it makes it clearer how to do the multiplication.
First, multiply 1.2 by 3.4 -- mumble, mumble...ok, that's 4.08. Now, multiply
10 
by
10 
. That may seem complicated, but remember our discussion earlier about
powers of 10 (in Section 1.3). To multiply 10 by 10 ,
all you have to do is add up the exponents, which is 6 + 7 = 13 here, to
figure out that 
. So here's how the calculation
works:
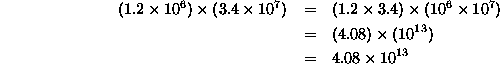
So the answer to the question ``what is
?'' is 
.
Division works similarly. Here's an example: what is
?
Here, you divide things up the same way, so you get
So the only big worry is what is 
? Remember from our
discussion of powers of 10 (in Section 1.3) that to divide
numbers that are powers of 10, all you have to do is subtract the exponents?
In this example, that means 9 - 3 = 6, so 
.
So, what's the answer to our question?
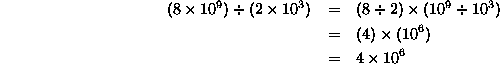
So the answer is 
.
These are all small examples, and you might say, ``Ack! I'll just multiply the way I'm used to!'' Don't panic. Think about this: what if I ask you to multiply 1,111,000,000,000,000,000,000 by 5,000,000,000,000,000,000? This looks nasty, but remember to do it in scientific notation, just like this:
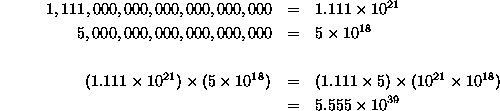
which is 5,555,000,000,000,000,000,000,000,000,000,000,000,000. Just imagine doing that on paper, longhand! Yuck.