How does the heat escape?

Why does the seafloor deepen with age?

What forces drive the plates?

* Review global topography, earthquakes, and subduction (Chapter 6)

The vertical flow of wax blobs in a lava lamp illustrates the three main modes of heat transport, radiation, convection, and conduction. These also important heat transfer mechanisms in the Earth so it us useful to understand the physics of the Lava Lamp. Examine the diagram and try to answer the 7 questions.

1) Where does the electricity come from? (several answers). [Electrical energy comes from the generators at the electric company. Turbines are driven by either the burning of fossil fuel (oil, gas, or coal), nuclear power, hydroelectric power, geothermal power or wind energy. There is a good discussion of resources in the Blue Planet - Chapter 17.]

2) Why does the bulb glow? [Current flowing through the tungsten filament inside the light bulb causes the atoms to collide at high speed. The filament becomes heated to a temperature of more than 2000 degrees centigrade and it radiates energy in the visible part of the spectrum. See page 55 of Blue Planet.]

3) How does the heat get from the bulb to the wax? Would this work in a vacuum? [The radiation travels as light waves from the filament through the vacuum inside of the bulb, through the glass walls of the bulb and into the lamp where it is absorbed in the dark colored wax.]

4) What happens to the wax when it heats up? (two answers) [First it melts changing from a solid phase to liquid phase; this allows it to flow. Second, it expands with increasing temperature; this provides buoyancy]

5) Why does the lower blob rise? [At a high enough temperature it becomes less dense than the colorless fluid and ascends toward the top of the lamp.]

6) Why does the lower blob fall? [During ascent the blob loses heat by conduction to the surrounding fluid and radiation out of the lamp. Eventually, the wax cools and shrinks enough to become more dense than the clear fluid and it begins to fall toward the bottom.]

7) What are the three types of heat transport mechanisms in operation? [radiation of visible electromagnetic radiation and propagation of waves (or photons) from lamp to wax, convection from bottom to top of lamp, and conduction of heat from clear liquid through the glass walls.]

How can we measure the age of the Earth? How long has it been since the solar system condensed from a nebular cloud? What keeps the Earth from freezing? What is the energy source for plate tectonics? The answers to all of these questions is related to decay of radioactive isotopes of uranium-U, thorium-Th, and potassium-K.

Back in the late 1800's before radioactivity was discovered, Lord Kelvin did a simple calculation to estimate the age of the Earth.

* Assume the Earth started out as a hot ball of rock at 1200 degrees centigrade.

* Assume the surface of the earth is at a constant temperature of 0 degrees centigrade. (Why is 0 C a good number? What is the temperature at the bottom of the ocean? What is the boiling point of water?)

* Go out and measure the present geothermal gradient which is the rate of temperature increase with depth in the Earth.

* Use heat conduction theory to estimate the amount of time it would take to go from the initial high temperature state to the present state.

This simple calculation provided an estimate of the age of the Earth of only 10 million years with an upper bound of 24 million years. The geologists at that time had estimated the age of the Earth to be greater than several hundred million years old. Their estimates were based on qualitative evidence such as deposition rates in sedimentary basins an guesses at the rate of the evolution of life forms. Of course, the age of the Earth is actually 4.6 billion years so Kelvin was wrong and the geologists were right. What was wrong with Kelvin's calculation?

The problem was that he did not know about radioactive heating. In 1896 when radioactivity was discovered, Rutherford identified the error in Kelvin's model; Kelvin did not include the heat supplied by radioactive decay of U, Th, and K. This same process also provides a means for dating rock samples and for measuring the age of the Earth.

Uranium to Lead

Lets examine the isotope of uranium that has an atomic weight of 238.

First U²³⁸ undergoes an alpha-emission as follows:

U²³⁸ > Th²³⁴ + alpha particle + gamma-ray + heat.

An alpha particle has 2 protons and 2 neutrons.

This is followed by a series of beta emissions.

A beta emission is a neutron that ejects an electron to form a proton.

Ultimately the uranium 238 is converted to lead-Pb 206 and heat. The half life of this reaction is 4.5 billion years. (see uranium decay series)

A Simple Differential Equation

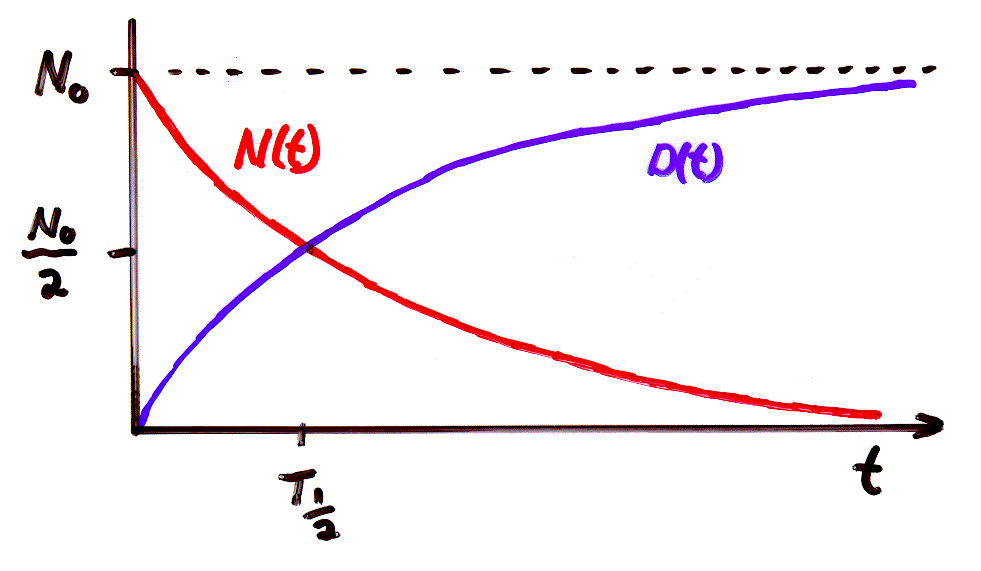
Radioactivity follows a very simple differential equation. [A differential equation is like an ordinary algebraic equation but one of the terms contains a derivative.] Here is the problem. We have a block of a radioactive isotope containing N atoms of parent material- say U²³⁸ and D atoms of daughter material say Pb²⁰⁶. Before any parent atoms disintegrated there were N_o = N + D parent atoms. The disintegration rate is proportional to the decay constant and the number of atoms that have not yet disintegrated N. Please go through the following math and convince yourself that the number of parent atoms decrease exponentially with increasing time.

Here is a good exam question. Suppose the fraction of parent N atoms to the original number of parent N_o atoms is 1/8. How many half lives have occurred? The answer is 3.

Dating a Rock

This description of determining the age of a rock is oversimplified but it contains the important ideas. Lets take a block of pure U²³⁸ and let it sit for some time t. We can use a mass spectrometer to measure the ratio of daughter to parent atoms. Then if the dacay constant is known, we can plug into the above formula to establish the age of the uranium/lead block.

The situation is slightly more complex for dating a real rock because we need to first define what we mean by age (e.g. age of crystallization , the age of exposure on the surface of the earth, the age of metamorphism . . .). Moreover, one should match the half-life of the isotope used for dating to the time scale of interest. For example when measuring the age of an ancient tree one would use a different isotope such as carbon 14. Many dating methods used in geology, archeology and other fields rely on this simple physics and the differential equation given above.

Planetary Heating

For this lecture, radioactivity is important because provides the heat source to keep the Earth from freezing and to maintain the plate motions of plate tectonics. There are four important isotopes that are abundant in the mantle and have half-lives comparable to the age of the Earth. They are U²³⁸, U²³⁵, Th²³² and K⁴⁰.

The following diagram shows the total heat generation in the mantle as a function of time before present. Today the total geothermal output (see Blue Planet, page 15)is 3x10¹³ W which is about 10 times the US energy consumption rate. In the past heat generation in the Earth was more than 4 times higher. The implication is that the plate tectonic activity must have been more vigorous in the past to maintain the heat flux.