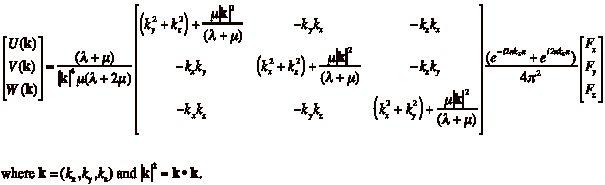Analytic 3-D Viscoelastic Body
Force Model
Smith and Sandwell [in preparation]
Our full deformation model consists of a
body-force couple (fault) embedded in an elastic plate overlying a viscoelastic
half-space (Figure 1). We begin by solving for the
displacement vector u(x,y,z) due to a point vector body force at depth. Arbitrarily complex curved and
discontinuous faults are generated in a fin grid of force vectors. We ignore the effects of EarthÕs
sphericity and assume a Poisson material while maintaining constant layer shear
moduli (rigidity) with depth. An overview of this solution follows:
(1) Derive differential equations relating a three-dimensional
(3-D) vector body force to a 3-D vector displacement. We apply a simple force balance in a homogeneous, isotropic
medium and after a series of substitutions for stress, strain, and displacement,
we arrive at Equation 1, where u, v, and
w are vector displacement components
in x, y, and z, l and m are Lame parameters, and rj
are vector body force components in an orthogonal system (i.e. j = x, y, or z):
(1)
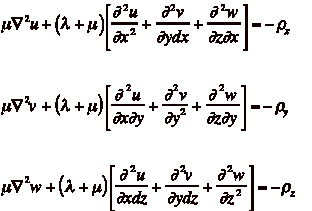
A vector body force is applied at 
, where we assume a sign convention such that z < 0 is considered downward from the surface and a is a negative number. To partially satisfy the boundary condition of zero shear
traction at the surface, an image source, identical to the initial source yet
mirrored in location above the z-axis,
is also applied at 
[Weertman,
1964]. Equation 2 describes a point body force at both source and
image locations, where F is a
vector force.
(2)
(2) Take the 3-D Fourier transform of Equations 1 and 2 to
reduce the partial differential equations to a set of linear algebraic
equations.
(3)
(3)
Invert the linear system
of equations to isolate the 3-D displacement vector solution for U(k), V(k), and W(k):
(4) Perform the inverse Fourier transform in the z-direction (depth) by repeated application of the
Cauchy Residue Theorem. In the
following equation, U(k,z) represents the deformation tensor, while subscripts s and i
refer to source and image contributions.
(4)
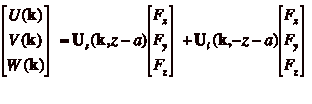
(5) Introduce
a layer into the system through an infinite summation of image sources. We
utilize the method of images [Weertman, 1964] and superpose multiple image sources [Rybicki, 1971], reflected both above and below the horizontal
axis, to account for both the source vector and the elastic layer, defined by
thickness H (Appendix B). The development of this solution
requires an infinite number of image sources to satisfy the stress-free surface
and layer boundary conditions (Equation 5). Contrasting layer and half-space rigidities m1 and m2,
respectively, are also included.
(5)
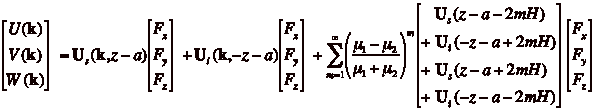
(6) Integrate the point source Green's function
to simulate a fault (Equation 6), where the body force is applied between the
lower depth d1 and the
upper depth d2. For a complex dipping fault, this
integration can be done numerically.
However, if the fault is vertical, the integration can be performed
analytically. The displacement or stress (derivatives are also computed
analytically) can be evaluated at any depth z above d2.
(6)
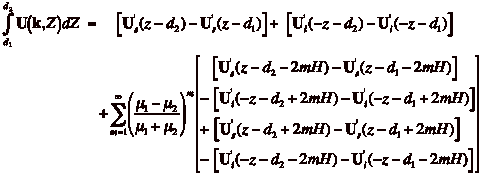
In Equation 6, 
is the
depth-integrated solution. The
individual elements of the source and image tensors are
(7)
,
where Z represents all z-dependent terms, including all
combinations of z, dn, and 2mH. The six independent functions of the
deformation tensor are
(8)
,
The solutions of Equation 8 are identical
to those of Smith and Sandwell
[2003] but have been simplified here for further manipulation of the
exponential terms. In particular,
we analytically sum the infinite series for the case of m2
= 0, which corresponds to the end-member case of an elastic plate over a fluid
half-space.
(7) Analytically solve
for Maxwell viscoelastic time-dependence using the Correspondence Principle.
The numerical components of this entire
approach involve generating a grid of force couples that simulate complex fault
geometry, taking the 2-D horizontal Fourier transform of the grid, multiplying
by the appropriate transfer functions and time-dependent relaxation
coefficient, and finally inverse Fourier transforming to obtain the desired
results. Our layered fault model
consists of an elastic plate overlying a Maxwell viscoelastic half-space (Figure 1)
that includes parameters of plate thickness (H), locking depths (d1, d2), half-space viscosity (h), elastic
moduli (E, m), density (r), gravity (g), and time (t). We simulate a finite-width single and
double force couple, F, with a
displacement discontinuity across the fault imbeded in a finely-spaced
grid. The analytic form of the
force couple is the derivative of a Gaussian function, where the half-width of
the Gaussian is equal to the cell spacing. As previously mentioned, our Fourier solution satisfies the
zero-traction surface boundary condition and continuity across the
boundary. The x-boundary condition of constant velocity difference
across the fault plane (for deeply defined slip) is simulated using a cosine
transform in the x-direction. The y-boundary condition of uniform velocity in the
far-field is simulated by arranging the fault trace to be cyclic in the y-dimension.
This fault model will be used to rapidly explore the realistic 3-D
viscoelastic response of the Earth throughout the earthquake cycle.