Following the elastic half-space derivation, we have developed a semi-analytic, time-dependent model for 3-D displacement and stress caused by a dislocation in an elastic half-space over a viscoelastic half-space. All solutions have been developed in the Fourier domain to exploit the speed of the convolution theorem. In addition, a new analytic solution has been developed following the Boussinesq Problem that satisfies the necessary surface and layer boundary conditions and also includes the restoring force of gravity.

We use this model to investigate the viscoelastic behavior of fault deformation for different stages of the earthquake cycle. The model consistis of an elastic lithosphere overlying a viscoelatic ashenosphere [Savage and Prescott, 1978] that is coupled by shear stress across the elastic-viscoelastic interface. Following an earthquake, ductile regions within the Earth respond to an instntaneous transfer of stress by solowly relaxing with time and transferring a shear load back onto the asthenosphere [Thatcher, 1983]. This short period of time-dependent deformation allows deeply focused stress to relax, ultimately reloading a locked fault and initiating the earthquake cycle sequence repeatedly. Elastic plate thickness, rheological constraints, and the role of gravity play a key role in 3-D velocity and stress behavior.

Model Formulation

3D Animations

San Andreas Fault System

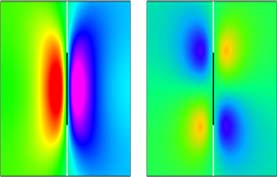
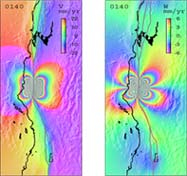
Future complex models, constrained by both geologic and geodetic observations of the San Andreas Fault System, will be establised in order to improve our understanding of temporal plate-boundary deformation and stress variations throughout the earthquake cycle.

Home

Elastic model

Viscoelastic model