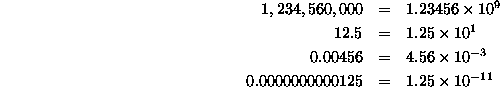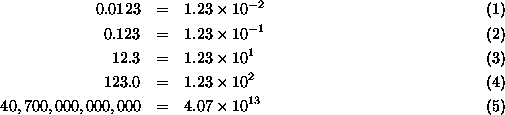
Scientific notation is a special kind of shorthand which scientists use when they need to talk about really big numbers or really small numbers (like the distance in miles to the nearest star other than the Sun - 40.7 trillion, or 40,700,000,000,000, kilometers) We will be using scientific notation in this class, and in case you've never seen it, I'll try to explain it here.
Below are some examples of numbers written ``normally'' and in scientific notation:
, N times 10 raised to a power M (called the
``exponent''). N is a value between 1 and 9.9999.... If the number x is less
than 1, the exponent is a negative number, and for numbers 1 or larger, the
exponent is a positive number. In
example 4 above, N is 1.23 and the exponent is 2, in scientific
notation is 
, which is usually read as ``1.23 times 10 to
the 2'' or ``1.23 times 10 to the second''.
A way to remember how to write numbers in scientific notation is to think about moving the decimal point in the number. What you do is slide the decimal point either right or left until there is one digit between 1 and 9 to the left of the decimal point, and count the number of ``slides'' you make. The number of slides is the exponent, while the value with the decimal point in it is what is multiplied by 10 to the exponent. You can figure out the sign of the exponent from which way you had to move the decimal point; if you move the decimal point left, the sign of the exponent is positive, and if you move the decimal point to the right, the exponent is negative.
If that sounds confusing, perhaps some examples will help. First, let's write
the number 123,000 in scientific notation. First, you slide the decimal point
to the left five times until you have 1.23000. You now know that the value N
is 1.23 and that M, the exponent, is +5 (since you slid the decimal point to
the left 5 times). So 
in scientific notation, and
it would be read ``1.23 times 10 to the fifth''.
Here's another example. Let's write the number 0.0000234 in scientific
notation. First, slide the decimal point to the right five times until you
have 2.34. You now know that in this case N is 2.34 and the exponent this time
is -5, since you slid the decimal point to the right 5 times. So
in scientific notation, and would be read
``2.34 times 10 to the -5''.
Now, you can of course translate ``backwards'' from scientific notation to
``normal'' notation. To do that, you just reverse the way we got scientific
notation from ``normal'' notation. Let's say I ask you to translate the number
into ``normal'' notation. In this case, N is 4.56 and M,
the exponent, is +5. Since you are translating from scientific notation
to ``normal'' notation, you would move the decimal point to the
right 5 spaces. What you get is 456,000, so you know that
(read ``4.56 times 10 to the fifth'') is 456,000.
Now, let's translate the number 
. Again, N is 4.56, but
this time, the exponent is -6. Since you are translating back to
``normal'' notation, you would slide the decimal point to the left by 6
spaces. The number you get is 0.00000456, and so you know that
.
I'll let you write out 
. Not really -- don't do
that, it'll take a really long time.
Here are some further examples to try to help you with scientific notation:
