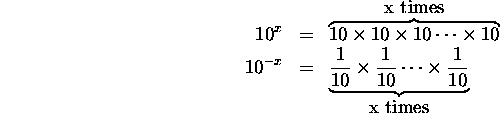
The decimal system, which is based on the number 10, is the number system used most in the world. Other number systems you are familiar with are binary numbers, which are based on zero and 1 and are used in computers, and time, which is divided (mostly) into units that are multiples of 60 - there are 60 seconds in a minute and 60 minutes in an hour, for example. Since the decimal system and powers of 10 are so important in science, I'll talk a bit about them here.
Don't panic about the phrase ``powers of 10'' - you are already used to using them, even if you aren't aware of it. Quick - what's 10 × 10? 100, of course. And what's 10 × 1/10? It's 1. These are simple examples to show you that you already know how this works.
Powers of ten are written like 10x, where x is whatever power I'm talking about and is called the ``exponent''. 10x means ``10 × 10, x times.'' 10-x means ``1/10 × 1/10, x times.'' In math, not words, it looks like
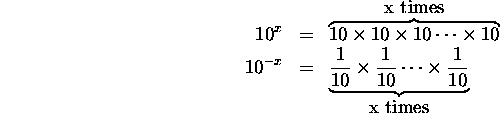
Here are a couple examples to make it a bit clearer:
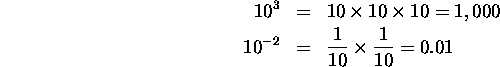
Table 1 lists numbers in both common notation and math notation. Some powers of ten are used frequently in science, and have special ``prefixes'', which are listed as well. Also, some powers of ten have been given names, some of which are no doubt familiar to you; I've put the names in the table.
If you look at Table 1, you may notice something useful: the exponent for each entry in the table is equal to the number of zeros in the corresponding number written ``normally''. That makes it easy to remember what a given power of ten is when written in the usual way. You may also be able to see why scientists and engineers prefer to write things like 1020, rather than write out a 1 followed by 20 zeros (100 000 000 000 000 000 000) -- it's shorter. We will talk more about scientific shorthand later, when we talk about scientific notation.
The ``prefix'' in the fifth column in Table 1 is used as a shorthand when talking about numbers of things. For example, computer memory is usually measured in Megabytes, or millions of bytes, and computer hard disk storage is now often measured in Gigabytes, or billions of bytes. Also, you might get a prescription for a cold medicine which is, say, 20 milligrams of some drug. That's a shorthand way of saying 20 thousandths of a gram.
Maybe you're not convinced that it's useful to be able to write numbers in powers of ten. Well, powers of ten are helpful when doing math, as well. Let's say I ask you ``what is 10 times 1,000?'' Not a big deal - it's just 10,000. But what if I asked you ``what is one trillion times one quadrillion?''
It turns out that multiplication of really big numbers is easy with powers of ten. All you have to do is add up the exponents, and you're done. Let's use the example I just gave you. What is one trillion times one quadrillion? First, using Table 1, you can see one trillion is 1012, and one quadrillion is 1015. So the answer is 1027. which is a really big number - and you can see that almost immediately, without needing a calculator or a piece of paper to do it longhand. Here are some more examples:
![]()
Division works similarly, except that you subtract the exponents. What is one trillion divided by one quadrillion? Well, it is 1012 ÷ 1015, so the answer is 10-3, or one thousandth. Here are some more examples:
![]()
Again, while this may not seem useful for small numbers, imagine dividing one trillion trillion trillion, which is 1036, by one thousand million billion, which is 1018, longhand. It would take you a while. (By the way, the answer is 1018.)
You may be wondering if there's an opposite to powers of 10; something like how division is the opposite of multiplication or subtraction is the opposite of addition. It turns out that there is just such a thing: logarithms, or ``logs''. It used to be that logs were really important for multiplying and dividing, and were used all the time in doing arithmetic using slide rules. Now that hand calculators are commonplace, the use of logarithms for basic calculations is fading away, but it can still be worthwhile. And while using logarithms for simple arithmetic is uncommon, there are other uses for logarithms in many areas of science, and we may see some of these uses later in the class.
The logarithm (log) of a number written as a power of ten is easy to calculate. It's just the exponent. So, for example, the log of 103 is 3. The log of 10-2 is just -2. And swapping that around is also easy: if I tell you the log of some number is 6, all you have to do is say the number is 106, or one million. Some more examples:
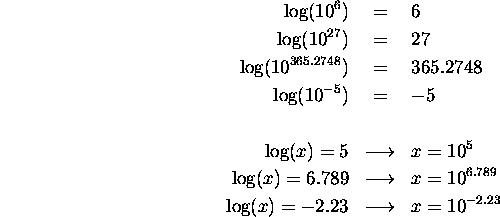
Where logs are really useful is in doing multiplication and division of numbers. You know from the previous section that to multiply numbers which are powers of ten, you add the exponents, and to divide such numbers, you subtract the exponents. Well, since the log of a number which is a power of 10 is just the exponent for that power, to do multiplication, you just add the logs. To do division, just subtract the logs. An example:
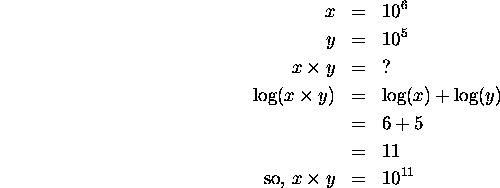
You could have seen the answer from Section 1.2, but you can see how easy it is to do this using logs. And so you can probably see why, back before powerful computers, logarithms made complicated computations simpler. As I said, few people do multiplication this way anymore, but it can be done.
If you have a basic scientific calculator, you will have a button on it somewhere that looks like ``10x''. That's the button to make a power of 10. You just enter a number, say 5, and hit the ``10x'' button, and the number you get back will be 105, or 100 000. In some cases, if you enter a big number, such as 50, and hit the 10x button, you won't see a 1 followed 50 zeros, but something which looks like ``1 E 50'' or ``1 EE 50''. Don't panic - that's just your calculator's version of scientific notation, which we will talk about in the next section.
Also on scientific calculators, you will find a button for doing logs - it's usually written ``log'', and is often very near the button for doing 10x. You just punch in a number, say 1 000 000, and hit the ``log'' button, and you will get the log of a million, which is 6.
Greg Anderson