Question 1. Write the following numbers as powers of ten. (4 points)
Question 2. Write the following numbers in ``normal'' notation. (4 points)
Question 3. Do the following problems. (4 points)
Question 4. Write the following numbers in scientific notation. (4 points)
Question 5. Write the following numbers in ``normal'' notation. (4 points)
Question 6. Perform the following calculations. Show your work for full credit. (4 points)
which is wrong. A simpler example:
3 ÷ (5 × 12) = 3 ÷ 60 = 0.05
Clearly, 7.2 does not equal 0.05, but that's the sort of mistake you will make if you multiply (5.05 × 10-10) and (1.10 × 10-8) first, and then divide (2.55 × 105) by the result of the multiplication. You should do the math in order from left to right, like this:
Question 7. (8 points)
Answer: $600
A few people had problems with 7, but not many. Here's how to do it:
You were traveling at 4470 cm/sec. You need to convert that to m/sec in order to figure out how many m/sec above the speed limit you were driving. To do that:
44.7 m/sec - 31.3 m/sec = 13.4 m/sec
So you were driving 13.4 m/sec over the speed limit. Now, since I gave you the fine in dollars per mile/hour over the speed limit, you need to convert from m/sec to miles/hour. To do that:
The number 1609 meters = 1 mile was given in Section 3.1 of Handout 1. The number 3600 sec = 1 hour can be easily computed from the fact that there are 60 seconds in a minute and 60 minutes in an hour.
Finally, you need to multiply the fine in dollars per mile/hour by the number of miles/hour you were driving over the speed limit, which gives you
Since you were asked to round your number to the nearest dollar, you should tell your buddies to scrounge up $600 to get you out of jail. You might have to wait a while (at least if you have poor friends like I do).
Question 8. (8 points)
Answers: (a) 122 beers; (b) 86 ¢
OK, so my beloved San Francisco 49ers lost to the fundamentally evil (second only to the Dallas Cowboys on the evil-ness scale) Green Bay Packers, and all the cheeseheads went even more nuts than they were. Note that I didn't say the Packers beat the 49ers, since the 49ers played like #*@#$&... At any rate, the problem still works.
A few people had problems with part (a). Here's how it works:
First, you need to convert from 15.3 gallons to ounces and then divide the number of ounces by 16 to get beers.
1958.4 ounces/(16 ounces/beer) = 122.4 beers
I asked you to round your answer to the nearest beer, so you would report that you can get 122 16-ounce beers from a 15.3 gallon keg, assuming you can get all the beer out and not allowing for the beer to form a head in the glass.
A surprising number of people had trouble with part (b). Here's how it works:
You simply need to divide the total cost of the keg by the number of beers, and then round.
So the beers will cost you 86 cents each. If I were having the party, though, I'd charge $2 each and then make about $140 profit (for pizzas, of course).
And Go Denver!
Question 9. The Age of the Universe (50 points)
Answer: about 1.5 × 1010 or 15 billion years.
This was the hardest problem, and it was also the one that gave the most trouble to the most people, but even so, most folks did pretty well.
Before I go into how to do this problem, I'd like to tell you a little bit about why this problem is important. You can read a lot more about it on the quite nice Origin of the Universe Web Page by Ann Gile, Carrie Hess, and Steve Lee at Bowdoin College in Maine. I've abstracted the following from there and a good NASA Page on Edwin Hubble.
In 1917, Albert Einstein published a paper which used his Theory of General Relativity and a new addition called the cosmological constant to argue that the universe was static and unchanging. I don't know why Einstein wanted such a universe, but he worked hard to get one.
Later, in 1922 and 1927 respectively, a Russian named Alexander Friedmann and a Belgian named Georges Lemaître demonstrated that there was a solution to Einstein's equations which did not require the cosmological constant. However, it also was not a static universe - it was an expanding universe. Such a universe could either continue to expand forever, or could collapse at some point in the future. More importantly for our worldview, in my opinion, is the fact that a universe which is expanding can have a definite beginning. Quite shocking for a populace which largely believed the universe was created as it is today.
So which was it? Static or expanding, created as is or beginning at some finite time?
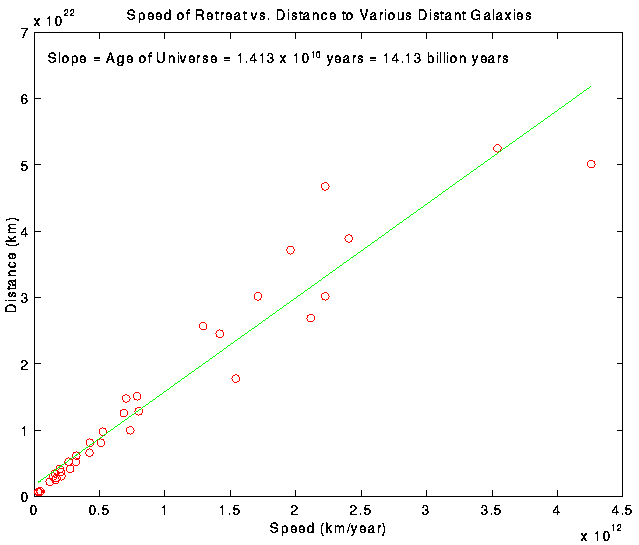
In 1929, a scientist named Edwin Hubble stunned the cosmological world with a paper in which he announced that he had discovered that the distances to faraway galaxies were directly related to the apparent redshifts of those galaxies, and that galaxies which were farther away from us were moving faster than galaxies closer to us. With this figure, he demonstrated that the universe must be expanding. Einstein could not be right, and Friedmann and Lemaître had to be at least partially right. Furthermore, he proved that universe could not have always existed as it is today, and must have been formed at some time in the past and evolved into the form in which the universe exists today. Quite an upheaval from such a simple figure.
OK, so what does all this have to do with your homework? Well, you have just repeated Hubble's calculations. The graph you made in doing this homework is essentially the same as the graph which Hubble published which demonstrated the expanding universe. Think about that for a moment: you've just done a problem which proves the universe must be expanding and evolving. Pretty astounding, if you ask me.
First, you need to convert from cm to km (for distance) and then from cm/sec to km/year (for speed). If you consult Table 1 of Handout 1, you will note that ``c'' is the abbreviation for ``centi'', meaning 0.01; also you will note that ``k'' is the abbreviation for ``kilo'', meaning 1000. So ``cm'' is 0.01 meters and ``km'' is 1000 meters. So here's the conversion:
So there are 0.00001 centimeters in one kilometer. Next, you need to convert from cm/sec to km/year. Here's the conversion:
1 cm = 0.00001 km
1 cm/sec × 1 sec/(3.16888 × 10-8 years) × 0.00001 km/1 cm = 3.15569 × 102 km/year or 315.569 km/year
So 1 cm = 0.00001 km and 1 cm/sec = 315.569 km/year.
Next, you need to apply those conversions to the numbers in Table 1 of Homework 2, and you will get numbers which look like the ones in my table of converted values.
Most people had no trouble with any of the stuff above. The major problem for most people came when they wanted to plot their graphs. Since the numbers in my table of converted values have a very large range, one has to be careful in plotting them. Two mistakes were made commonly:
The only answer I can give those folks is, well, that's just how they are going to look - all scrunched up. There will be lots of points grouped together in the lower left corner of the graph. That's just the way it is.
The problem that these folks had was that they tried to make the tick marks evenly spaced, when the numbers with which they labeled their tick marks are not evenly spaced. As an example, I often saw graphs with tick marks labeled in steps of 1 × 1010. This is a problem --- while the step from 1 × 1010 to 2 × 1010 can be used nicely for 1 × 1010 to 1 × 1011, the step from 1 × 1011 to 2 × 1011 must be 10 times bigger! And the step from 1 × 1012 to 2 × 1012 must be 100 times bigger than the step from 1 × 1010 to 2 × 1010, which means that the space between tick marks must be 10 and 100 times larger, as well.
This means that you either would have to have a verrrrrry long axis or you have to do something else. What I did was simply to make my tick marks at spacings of 50 × 1010, running from zero to 450 × 1010. This will mean, as in (1) above, that you will have a bunch of points all scrunched up in the lower left corner, but that is inescapable.
At any rate, your graph should end up looking like the one below (note the axis tick spacing):

I plotted the graph above using the software MATLAB, and had that program choose the best straight line through my points (using a somewhat complicated math procedure called ``least-squares fitting'') and plot it. My best straight line has a slope of 1.413 × 1010 or 14.13 billion years. This slope is my estimate for the age of the universe. Note that it's not exactly 15 billion years - that's just the way this set of numbers works...
Greg Anderson