?
Don't panic about the phrase ``powers of 10'' -- you are already used to using
them, even if you aren't aware of it. Quick -- what's 
? 100,
of course. And what's 
? It's 10. These are simple
examples to show you that you already know how this works.
Powers of 10 are written like , where x is whatever power I'm
talking about and is called the ``exponent''. means
``10 
10, x times.'' 
means
`` 
, x
times.'' In math, not words, it looks like
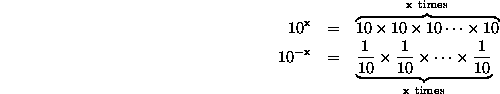
Here are a couple examples to make it a bit clearer:
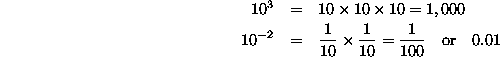
Below, I've made a table of powers of 10, both in math notation and common notation. Some powers of ten are used frequently in science, and have special names, which are called prefixes, that are used. I've got those prefixes in the table, too. Also, some powers of ten have cool names, some of which are no doubt familiar to you; I've put the names in the table as well.
Now, if you look at Table 1, you will notice something useful:
the exponent for each entry in the table is equal to the number of zeros in
the corresponding number written ``normally.'' That makes it easy to remember
what a given power of ten is when written in the usual way. But I think you
can also see why mathematicians and scientists prefer to write things like
rather than write out a 1 followed by 20 zeros, like
100,000,000,000,000,000,000 -- it's shorter. We will talk more about shorthand
later, when we talk about scientific notation.
The ``prefix'' in the fifth column in Table 1 is used as a shorthand when talking about numbers of things. For example, computer memory is usually measured in megabytes, or millions of bytes, and computer hard disk storage is now often measured in gigabytes, or billions of bytes. Also, you might get a prescription for a cold medicine which is, say, 20 milligrams of some drug. That's a shorthand way of saying 20 thousandths of a gram.
