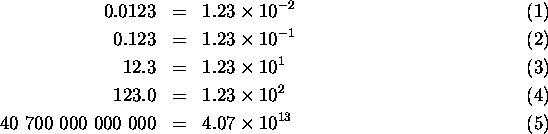
Scientific notation is a special kind of shorthand which scientists and engineers use when they need to talk about really big numbers or really small numbers (like the distance in miles to the nearest star other than the Sun-40.7 trillion, or 40 700 000 000 000 kilometers). We will be using scientific notation in this class, and in case you've never seen it, I'll try to explain it here.
Below are some examples of numbers written ``normally'' and in scientific notation:
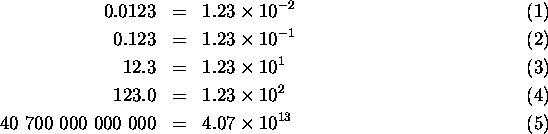
As you can see, in general a number x written in scientific notation has the form N × 10M, N times 10 raised to a power M (called the ``exponent''). N is a value between 1 and 9.9999... . If the number x is less than 1, M is a negative number, and for x 1 or larger, M is a positive number. In example 4 above, N is 1.23 and M is 2, and the number in scientific notation is usually read as ``1.23 times 10 to the 2'' or ``1.23 times 10 to the second''.
A way to remember how to write numbers in scientific notation is to think about moving the decimal point in the original number. What you do is slide the decimal point either right or left until there is one digit between 1 and 9 to the left of the decimal point, and count the number of ``slides'' you made. The number of slides is M, while the value with the decimal point in it is N. You can figure out the sign of M from which way you had to move the decimal point; if you move the decimal point left, M is positive, and if you move the decimal point to the right, M is negative.
If that sounds confusing, perhaps some examples will help. First, let's write the number 123 000 in scientific notation. First, you slide the decimal point to the left five times until you have 1.23000. You now know that the value N is 1.23 and that M is +5 (since you slid the decimal point to the left 5 times). So 123 000 = 1.23 × 105 in scientific notation, and it would be read ``1.23 times 10 to the fifth''.
Here's another example. Let's write the number 0.000 234 in scientific notation. First, slide the decimal point to the right four times until you have 2.34. You now know that in this case N is 2.34 and M this time is -4, since you slid the decimal point to the right 4 times. So 0.000 234 = 2.34 × 10-4 in scientific notation, and would be read ``2.34 times 10 to the -4''.
Now, you can of course translate ``backwards'' from scientific notation to ``normal'' notation. To do that, you just reverse the way we got scientific notation from ``normal'' notation. Let's say I ask you to translate the number 4.56 × 105 into ``normal'' notation. In this case, N is 4.56 and M is +5. Since you are translating from scientific notation to ``normal'' notation, you would move the decimal point to the right 5 spaces. What you get is 456 000, so you know that 4.56 × 105 (read ``4.56 times 10 to the fifth'') is 456 000.
Now, let's translate the number 4.56 × 10-6. Again, N is 4.56, but this time, M is -6. Since you are translating from scientific notation to ``normal'' notation, you would slide the decimal point to the left by 6 spaces. The number you get is 0.000 004 56, and so you know that 4.56 × 10-6 = 0.000 004 56.
Here are some further examples to try to help you with scientific notation:
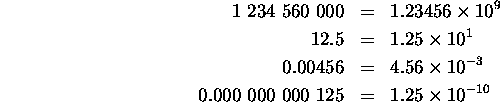
Numbers written in scientific notation are still just numbers, so of course you can do math on them. Doing math using scientific notation seems more complicated than the usual method when you've never done it before, but after a little practice, it's actually easier. That's particularly true for multiplication and division, so we'll skip addition and subtraction and go straight to multiplying and dividing.
Let's look at an example. What is (1.2 × 106) × (3.4 × 107)? To answer this question, first let's shuffle the numbers a bit:
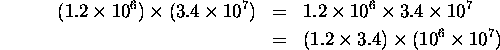
Nothing fancy here, but I think it makes it clearer how to do the multiplication. First, multiply 1.2 by 3.4 - that's 4.08. Now, multiply 106 by 107. That may seem complicated, but remember our discussion about powers of ten in Section 1.2. To multiply 106 by 107, all you have to do is add up the exponents, which is 6 + 7 = 13 here, to figure out that 106 × 107 = 1013. So here's how the calculation works:
Division works similarly. Here's an example: what is (8 × 109) ÷ (2 × 103)? Here, you divide things up the same way, so you get
So the only big worry is: ``what is 109 ÷ 103?'' Remember from our discussion in Section 1.2 that to divide numbers that are powers of ten, all you have to do is subtract the exponents. In this example, that means 9 - 3 = 6, so 109 ÷ 103 = 1013. So, what's the answer to our question?
These are all small examples, and you might not be convinced that any of this is actually useful. But what if you had something harder? For example, say I ask you to multiply 1 111 000 000 000 000 000 000 by 5 000 000 000 000 000 000? This looks nasty, but remember to do it in scientific notation, just like this:
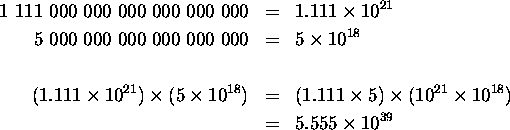
which is 5 555 000 000 000 000 000 000 000 000 000 000 000 000. Just imagine doing that on paper, longhand.
If you have a scientific calculator, you can do scientific notation on your calculator. If you look around, somewhere on the calculator, there will be a button which says something like ``EXP'' or ``EEX'' or ``EE''. That button is for entering numbers in scientific notation.
On my HP calculator, the button is ``EEX'', and to enter a number like 1.23 × 1033, I type ``1.23 EEX 33'' into my calculator. I get out something which reads ``1.23 E 33''. That ``E 33'' part stands for 1033. On my friend Kevin's Casio calculator, the button is ``EXP'', and to enter 1.23 × 1033, I type ``1.23 EXP 33'' into the calculator. I get back something which reads `` 1.2333''. The small ``33'' in the upper right corner of the screen is the Casio's version of 1033.
All scientific calculators have some way of doing this, and all of them will display something like ``1.23 EE 33'', ``1.23 E 33'', or ``1.2333'', or something very similar. Once you have the numbers you want in your calculator in scientific notation, of course you can do the usual multiplying, dividing, adding, subtracting, taking square roots, squaring, or whatever, just as you would for a number displayed ``normally''.
Scientific notation is really just a shorthand version of writing really big or really small numbers. No working scientist uses scientific notation for every number - numbers like 1,000 or 0.01 are small enough and simple enough to write that they would be written just like that. But a working scientist would certainly not write out 40 700 000 000 000 kilometers in a paper - it's just too long! Instead, she would write the number as 4.07 × 1013 kilometers - which is easier to write. (In fact, she'd probably write 4.07 × 1013 km, since ``km'' is the abbreviation for kilometers.) Similarly, she wouldn't write out 0.000 000 000 000 000 002 356. She would instead write out 2.356 × 10-18, which again is easier on everyone. And scientific notation can make some kinds of math problems more manageable. Doing arithmetic on really big or really small numbers is much simpler, once you know how to use scientific notation.
Greg Anderson