Bridget Smith and David Sandwell
J. Geophy. Res., 2003
Quick Contents:
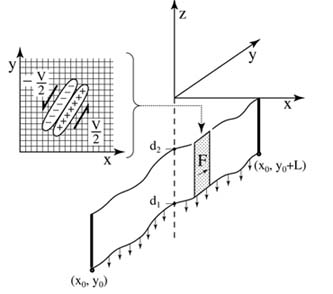
For the last several decades, the most commonly used analytic models of fault-induced deformation have been based on the dislocation solutions of Chinnery [1961, 1963], Rybicki [1973], and Okada [1985, 1992]. The latter provide analytic expressions for stress, strain, and displacement in an elastic half-space due to a displacement discontinuity. While these dislocation models are accurate and computationally efficient when applied to individual faults or small fault systems, they may become computationally prohibitive when representing fault geometry over the entire North American-Pacific plate boundary. However, if model calculations are performed in the spectral domain, the computational effort is substantially reduced. Rather than calculate the Fourier transform of the analytic solutions mentioned above, we instead solve the 3-D elasticity equations in the wave-number domain and then inverse Fourier transform to obtain space domain solutions.
To summarize our analytic approach, the elasticity equations are used to derive a set of transfer functions (in the wave-number domain) for the 3-D displacement of an elastic half-space due to an arbitrary distribution of vector body forces. The numerical components of this approach involve generating a grid of force couples that simulate complex fault geometry, taking the 2-D Fourier transform of the grid, multiplying by the appropriate transfer function, and finally inverse Fourier transforming. The force model mus be designed to match the velocity difference across the plate boundary and have zero net force and zero net moment
Model Formulation
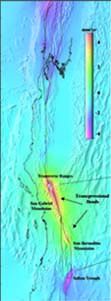
San Andreas Fault System

Home
Elastic model
Viscoelastic model